Self-evolving artificial intelligence framework to better decipher short-term large earthquakes – Scientific Reports

Seismogenesis agent and environment

There are two analogous entities between the real-world seismogenesis and the proposed RL, i.e., seismogenesis agent and environment (Fig. 1A). In general RL, given the present state (\(S^{(t)}\)), an “agent” takes actions (\(A^{(t)}\)), obtains reward (\(R^{(t+1)}\)), and affects the environment leading to next state (\(S^{(t+1)}\)). These terminologies are defined in typical RL method and their analogies to the present framework are summarized in Fig. S1. The “environment” resides outside of the agent, interacts with the agent, and generates the states. In this study, a “seismogenesis agent” is introduced as the virtual entity that can take actions according to a hidden policy and determines all future EQs. The seismogenesis agent’s choice of action constantly determines the next EQ’s location, magnitude, and timing given the present state and thereby affects the surrounding environment. In this study, “environment” is assumed to include all geophysical phenomena and conditions in the lithosphere and the Earth, e.g., plate motions, strain and stress accumulation processes near/on faults, and so on. We can consider the Markov decision process (MDP) in terms of a sequence (or trajectory) and the so-called four argument probability \(p:\mathcal {S}\times \mathcal {R}\times \mathcal {S}\times \mathcal {A}\rightarrow \mathbb {R}[0,1]\) as

According to the “Markov property”⁴⁵, the present state \(S^{(t)}\) is assumed to contain sufficient and complete information that can lead to the accurate prediction of the next state \(S^{(t+1)}\) as would be done by using the full past history. As shall be described in detail, the reward is rooted in the prediction accuracy of future EQs in terms of loci, magnitudes, and timing, and thus the true seismogenesis agent can always receive the maximum possible reward since it always reproduces the real EQ. The “true” seismogenesis agent remains unknown and so does the policy. The primary goal of the proposed RL is to learn the hidden policy and to evolve the agent so that it can imitate the true seismogenesis agent as closely as possible. Thus, as evolution continues, the RL’s agent pursues the higher reward (i.e., the long-term return) and gradually becomes the true seismogenesis agent. There are notable benefits of the adopted RL. First, with incoming new data, improving the new features and transparent ML methods will be autonomously done by RL, without human interventions. Second, RL will search and allow many pairs of state-action (i.e., current observation-future prediction), and thus researchers may obtain with uncertainty measures many prediction rules that are “customized” to different locations, rather than a single unified prediction model. In essence, the proposed global RL framework will act as a virtual scientist who keeps improving many pre-defined control parameters of ML methods, keeps searching for a better prediction rule, and keeps customizing the best prediction rule for each location and new time.

Information fusion core

As shown in Fig. 1C, the framework’s first core is the information fusion core that can transform raw EQ catalog data into ML-friendly new features—convolved information index (II) which can quantify and integrate the spatio-temporal information of all past EQs. The term “convolved” II is used since this core mainly utilizes a sort of convolution process in the spatial and temporal domains of the observed raw EQ data in the lithosphere. By extending convolution to the time domain, this core quantifies and incorporates cumulative information from past EQs, creating spatio-temporal convolved II ( \(\overline{II}_{ST}^{(t)}\)), which is denoted as “New Feature 1” in this framework. Detailed derivation procedure is given in Supplementary Materials and Table 1.

State generation core

The second core of the framework is to generate and determine “states” (Fig. 1C). For RL to understand, distinguish, and remember all the different EQs across the large spatio-temporal domains, the state should be based on physics and unique signatures about spatio-temporal information of past EQs. Also, the effective state should be helpful in pinpointing specific location’s past, present and future events. To meet these criteria, this core defines “point-wise state” at each spatial location \(\xi _i\) in terms of the pseudo physics (\(\mathcal {U}\)), the Gauss curvatures of the pseudo physics (\(\mathbb {K}\)), and the Fourier transform-based features of the Gauss curvatures (\(\mathbb {F}\)) as defined in Eq. (3). Since \(n(\mathcal {U})=4, n(\mathbb {K})=8,\) and \(n(\mathbb {F})=160\), a state vector \(S_j\) has \(n(S_j) = 172.\) “New Feature 2” is defined as the high-dimensional, pseudo physics quantities (denoted as \(\mathcal {U}\)) using the spatio-temporal convolved IIs (i.e., New Feature 1) of the information fusion core. “New Feature 3” is defined as the Gauss curvature-based signatures (\(\mathbb {K}\)) that consider distributions of the pseudo physics quantities \(\mathcal {U}\) at each depth as surfaces. “New Feature 4” is defined as the Fourier transform-based signatures (\(\mathbb {F}\)) that quantify the time-varying nature of the Gauss curvature-based signatures \(\mathbb {K}\). Table 1 summarizes the key equations and formulas of the four-layer data transformations. With these multi-layered new features we can define “state” in the RL context as:

The primary hypothesis is that the “states” can be used as unique indicators of individual large EQs before the events, in hopes of enabling ML methods to distinguish and remember EQs. This core in essence infuses basic physics terms into new features. It should be noted that these physics-infused quantities are all “pseudo” quantities, derived from data, not from any known first principles. The author’s prior works^43,44 fully describe the generations of all the New Features. Its compact summary is presented in Supplementary Materials.

Prediction core

The main objective of the Prediction Core (Fig. 1C) is to select the best “prior” action (\(A^*\in \mathcal {A}^{(t)}\)) out of the up-to-date entire action set \(\mathcal {A}^{(t)}\) by using the policy (\(\pi \)) given the present state (\(S^{(t)}\)). The best action predicts the location and magnitudes of the EQ before the event (e.g., 30 days or a week ahead). This core leverages the so-called Q-value function approximation⁴⁵. Q-value function (denoted \(Q_\pi (S,A)\)) is the collection of future returns (e.g., the accumulated prediction accuracy) of all state-action pairs following the given policy. In this paper, Q-value function stores the error-based reward, i.e., the smaller error, the higher return. One difficulty is the fact that the space of the state set \(\mathcal {S}\) is a high-dimensional continuous domain, unlike the discrete action space. The adopted tabular Q-value function contains “discrete” state-action pairs. To resolve the difficulty and to leverage the efficiency of the tabular Q-value function, it is important to determine whether the present state \(S^{(t)}\) is similar to or different from all the existing states \( S^{(\forall \tau . For this purpose, the adopted policy uses the L2 norm (i.e., Euclidean distance) between states—e.g., \(S^{*}(S^{(t)}) :=\text {argmin}_{S^{(\tau )}} \Vert S^{(\tau )} – S^{(t)} \Vert _2, \forall \tau The L2 norm includes the state’s \(\mathcal {U}\) and \( \mathbb {K}\) but excludes \(\mathbb {F}\), for calculation brevity. Preliminary simulations confirm that the use of \(\mathcal {U}\) and \( \mathbb {K}\) appears to work favorably in finding the “closest” prior state \(S^*(S^{(t)})\) to the present state \(S^{(t)}\). For the policy \(\pi \) (i.e., the probability to select an action for the given state), this core leverages the so-called “greedy policy” in which the policy chooses the action that is associated with the maximum Q-value. Details about the formal expressions of the adopted policy and specialized schemes for this policy are presented in Supplementary Materials.

Internal searching process with the tabular Q-value functions used for the pseudo-prospective prediction by this framework 14 days before 2019/7/6 (\(M_w 7.1\)) Ridgecrest EQ: (A) The entire state sets stored in memory; (B) A tabular Q-value function identified to contain the closest state of the potential peaks. Vertical axis shows the reward of each state-action pair and outstanding spikes stand for the best actions of corresponding states. The last action is the dummy action that has the dummy reward as given by Eq. (14); (C) One specific Q-value function of actions and the state that is considered to be the potential peak. This process is used for all the pseudo-prospective predictions; (D) General illustration of a Jacob’s ladder for large EQ reproduction consisting of the state set with increasingly many pseudo physics terms and the action set (inspired by the Jacob’s ladder within the density functional theory⁴⁶). Raw EQs data are complex multi-physics vectors in space and time.

Action update core

Action update core seeks to find new action \(A^{*(t)}\) (i.e., prediction rules) when there are expanded states \(S^{(t)} \in \varvec{S}^{(ID)}, ID \ge 18\). This new action will be different from existing actions (\(A^{*(t)} \ne \forall A_i\in \mathcal {A}^{(t-1)}\)) already used in the Prediction Core. Since the state \(S^{(t)}\) is assumed to be “unique,” this core seeks to find a “customized” prediction rule (action) for each new state. In general, there is no restriction of the new action (i.e., new prediction rule/model). In the present framework, the Action Update Core leverages the author’s existing work, Glass-Box Physics Rule Learner (GPRL), to find the new best action (GPRL’s full details are available in⁴³). In essence, GPRL is built upon two pillars—flexible link functions (LFs) for exploring general rule expressions and the Bayesian evolutionary algorithm for free parameter searching. LF (\(\mathcal {L}\)) can take (i) a simple two-parameter exponential form or (ii) cubic regression spline (CRS)-based flexible form. As shown in^34,35,36, the exponential LF is useful when a physical rule of interest is likely monotonically increasing or decreasing with concave or convex shapes. In this framework, the pseudo released energy \(E_r\) takes the exponential LF due to the favorable performance⁴³. Also, GPRL can utilize CRS-based LFs for higher flexibility⁴⁷, which is effective when shapes of the target physics rules are highly nonlinear or complex. In this framework, the actions (prediction rules) take CRS-based LFs for generality and accuracy. The space of LFs’ parameters (denoted as \(\varvec{\uptheta }\)) is vast. Finding “best-so-far” free parameters \(\varvec{\uptheta }^*\) is done by the Bayesian evolutionary algorithm in this framework, as successfully done by^34,35,36. Table 2 presents the salient steps of the Bayesian evolutionary algorithm. All the new features (e.g., \(\overline{II}, \mathcal {U}, \mathbb {K}, \mathbb {F}\)) generated by the State Generation Core are used and explored as potential candidates in the prediction rules (i.e., actions). The best-so-far prediction rule’s expression identified by this framework is presented in Supplementary Materials. As shown by⁴⁴, the inclusion of the Fourier-transform-based new features \(\mathbb {F}\) appears to sharpen the accuracy of each prediction rule for large EQs (\(M_w \ge 6.5\)). It is noteworthy that the action (prediction rule) shares the same spirit as the so-called Jacob’s ladder within the density functional theory⁴⁶ in a sense that EQ reproduction accuracy gradually improves with the addition of more physics and mathematical terms (see Fig. 2D). Since the developed AI framework holds the self-evolving capability, whenever new large EQs occur, the old sets (State and Action) and Q-value functions should expand autonomously. The details about autonomous expansion of state, action, and policy are presented in Supplementary Materials.

Pseudo-Prospective Predictions by UCERF3-ETAS and Reproductions by the Present AI framework 14 days before 2019/7/6 (\(M_w 7.1\)) Ridgecrest EQ: (A) Real Observed EQ; (B) This AI framework’s best-so-far reproduction by the pre-trained RL policy; (C) ComCat probability spatial distribution from UCERF3-ETAS predictions of \(M\ge 5\) events with probability of 0.3% within 1 month time window; (D) ComCat magnitude-time functions plot, i.e., magnitude versus time probability function since prediction simulation starts. Time 0 means the prediction starting time. Probabilities above the minimum simulated magnitude (2.5) are shown. Favorable Evolution of New Action Learning: (E) Distribution of the entire rewards of “new” best actions given a new state set. The maximum reward \(\text {max}[r(S,A)]\) of the best-so-far prediction of the peak increases to 67.13 from 47.60 in (F) which shows the distribution of the entire rewards of “old” best actions given a new state set; Predicted magnitudes by using the new best action (G) whereas (I) is using the old best action. Compared to the real EQs (H), the new best action appears to favorably evolve (E,F).

Feasibility test results of pseudo-prospective short-term predictions

After training with all EQ catalog during the past 40 years from 1990 through 2019 in the western U.S. region (i.e., longitude in (− 132.5, − 110) [deg], latitude in (30, 52.5) [deg], and depth (− 5, 20) [km]), this paper applied the trained AI framework to large EQs (\(M_w \ge 6.5\)). The objectives of the feasibility tests are to confirm (1) whether the initial version of AI framework can “remember and distinguish” individual large EQs and take the best actions according to the up-to-date RL policy, (2) whether the best action can accurately reproduce the location and magnitude 14 days before the failure, and (3) whether RL of the framework can self-evolve by expanding its experiences and memory autonomously.

This feasibility test is “pseudo-prospective” since this framework has been pre-trained with the past 40 years’ data, identified unique states of individual large EQs, and found the best-so-far prediction rules. Each of the best prediction rules is proven successful in reproducing large EQ’s location and magnitude 30 days before the event as shown in the author’s prior work⁴⁴. It is anticipated that the framework should have “experienced” during training by which it can distinguish the individual events and can determine how to reproduce them using the best-so-far action out of the “memory,” the tabular Q-value function in this stage of framework. The objective of this feasibility test is to prove the potential before applications and expansions to the “true” prospective predictions in future research. Figure 2 schematically explains the process behind the RL-based pseudo-prospective prediction, starting from a new state, to Q-value function, and to the best-so-far action. Figure S29 presents some selected cases that confirm the promising performance of this framework. All other comparative investigations with large EQs (\(M_w \ge 6.5\)) during the past 40 years in the western U.S. are presented in Figs. S16 through S24. All cases confirm this framework’s promising performance compared to the EQ forecasting method. Particularly, in all pseudo-prospective predictions, RL can remember the states (i.e., the quantified information around the spatio-temporal vicinity of the large EQs during training) and also select the best actions (i.e., the customized prediction rules to the individual large EQs) from the stored policy.

As a reference comparison, a well-established EQ forecasting method UCERF3-ETAS^13,14,15,16 is adopted to conduct short-term predictions 14 days before the large EQs. This may not be an apple-to-apple comparison since EQ forecasting is not mainly designed for such short-term predictions of specific large EQs before the events. Still, this comparison meaningfully provides a relative standing of the framework showing its role and difference from the existing EQ forecasting approaches. Detailed settings of UCERF3-ETAS are presented in Supplementary Materials. Figure 3 compares the pseudo-predictions by UCERF3-ETAS and this framework. UCERF3-ETAS predicts large EQs in ranges of \(M_w \in [5,6)\) with 0.3% probability 30 days before the onset. Despite the low probability and the magnitude error, the spatial proximity of the prediction to real EQ is noteworthy, i.e., the distance between the dashed box and the real EQ (Fig. 3C). All EQs (\(M_w>3.5\)) of the past year are used as self-triggering sources of UCERF3-ETAS (Fig. 3D). In contrast, Fig. 3B confirms that this AI framework can remember the unique states of the reference volumes near the hypocenter of the Ridgecrest EQ, select the best-so-far action from the up-to-date policy, and successfully reproduce the peak of the real EQ 14 days before the failure. As expected, this framework’s reproduction of large EQs appears successful in achieving the threefold objective, i.e., accuracy in magnitude, location, and short-term timing. It should be noted that this framework does not remember any information on specific dates or loci of past EQs for training and prediction. Only the point-wise states near the large EQs are remembered. Also, the best actions associated with the states are stored as policy in terms of relative selection probabilities. At the time of the feasibility test, the framework accumulated about 110 important state sets and the associated 110 best actions. Thus, the feasibility test used the up-to-date RL policy stored in 110 tabular Q-value functions.

This performance of pseudo-prospective predictions is promising since searching for a similar (or identical) state from the storage is not a trivial task given a new state. Each time step (here, 1 day), there are \(n_s = \)253,125 reference volumes for the present resolution of 0.1 degrees of latitude and longitude, and 5 km depth. If we use all the point-wise states of the past 10 years, it amounts to \(10\times 365\times 253125\), i.e., approximately over 0.92 billion states. Figure 2 illustrates such a long RL searching sequence, starting from a new state, to Q-value function, and to the best-so-far action.

In some cases, UCERF3-ETAS appears to show promising prediction accuracy about epicenters’ loci, which can be also found in 1992/4/25 \(M_w 7.2\) EQ (Fig. S17C), 1992/6/28 \(M_w 7.3\) EQ (Fig. S17C), and 2010/4/4 \(M_w 7.0\) EQ (Fig. S20C). The common aspect of these cases is that they have relatively large prior EQs right before the prediction begins (time = 0), i.e., \(M_w \approx 6\) about 3 months earlier (Fig. S20D), \(M_w \approx 6\) about 50 days earlier (Fig. S17D), and \(M_w \approx 5.2\) about 40 days earlier (Fig. S16D). This may play favorably for the “self-triggering” mechanism of UCERF3-ETAS. but a general conclusion is not available since other cases do not support the consistent accuracy in loci of epicenters.

Self-evolution is the central feature of the present framework. Fig. 3E–I show how the new best action update can evolve in a positive direction. Given a new state (i.e., when a new large EQ occurs; Fig. 3H), “old” best action is used to predict the magnitudes which may not be accurate enough (Fig. 3I). Then, the Action Update Core seeks to learn “new” best action for the new state (Fig. 3G). Comparison of Fig. 3G and I clearly demonstrate the positive evolution of the new action, and Fig. 3E and F quantitatively compare the maximum reward of all state-action pairs. This example underpins that favorable evolution can take place by learning new actions.

Impact of new features on prediction rules

One of the key contributions of this paper is to generate new ML-friendly features that are based on basic physics and generic mathematics. It is informative to touch upon varying contributions of new features on the prediction rules. We conducted three separate training with 3 prediction rules that are

Model A (denoted by the author inside the program) utilizes the pseudo released energy and its power whereas Model B further harnesses pseudo vorticity and Laplacian terms. Model C, the prediction rule of this paper, uses Gauss curvature and FFT-based new features, as fully explained in Eq. (10) of Supplementary Materials. The detailed definitions and explanations about the terms in above models are presented in Supplementary Information. Figure 4 shows how the new features contribute to the prediction accuracy. All predictions are made 28 days before the real EQ event (Cape Mendocino EQ, \(M_w=7.2\), April 25, 1992) by using the best-so-far prediction rules. As clearly seen in Fig. 4B–D, the increasing addition of new features appears to boost the accuracy of the large EQ reproduction. Interestingly, the seemingly poor reproductions with Model A (i.e., pseudo released energy and power) and Model B (i.e., all four pseudo physics terms) still can capture the peak’s location. With the Gauss curvature and FFT-based new features (Model C, Fig. 4D), both location and magnitude are sharply reproduced. Naturally, the AI framework favors Model C over Models A and B. This comparison demonstrates that the new ML-friendly features hold significant impact on the accuracy on large EQ reproduction in magnitude, location, and short-term timing aspects. Also, it suggests that future extensions with more new features may substantially help improve the accuracy of the framework. Thus, the positive evolution of this framework appears possible, which warrants further investigation into new ML-friendly features.

Comparison of prediction rules with different new features: (A) Real observed EQ [Cape Mendocino EQ, \(M_w=7.2\), April 25, 1992]; (B–D) Reproduced EQ peaks by using the best-so-far prediction rules. (B) Model A uses the pseudo released energy and power whereas (C) Model B additionally uses vorticity and Laplacian terms (i.e., all four pseudo physics terms). (D) Model C is the rule presented by this paper in Eq. (10). All prediction rules are trained with the same hyperparameters and settings.

Conclusions and outlook

It is instructive to touch upon the optimality of the adopted approach. One of the primary goals of the RL is to find the best policy that leads to the “optimal” values of the states, i.e., \( v^*(s) :=\underset{\pi }{\text {max}}v_{\pi }(s), \forall s\in \mathcal {S}\). The “Bellman optimality equation”⁴⁵ formally states

where \(\pi ^*\) is the “global” optimal policy, q(s, a) is the action-value function meaning the expected return of the state-action pair following the policy, \(\gamma \) is the discount factor of future return, \(s’\) is the next state. In view of Eq. (6), this paper’s algorithm is partially aligned with the optimality equation, achieving the “local optimality.” To explain this, it is necessary to note what we don’t know and what we do know. On one hand, the transition probability \(\text {Prob}(s’,r|s,a)\) from the present state \(S^{(t)}=s\) to the next state \(S^{(t+1)}=s’\) is assumed to remain unknown and completely random (i.e., the hidden transition from past EQs to future EQ at a specific location). Also, the “global” optimal policy \(\pi ^*\) is not known at the early stage of learning. On the other hand, this paper seeks to use the best action for the given state (by Eqs. 12 and 13, thereby satisfying \({\text {max}}q_{\pi ^{(t)}}(s,a)\) of the 1st line of Eq. 6. Therefore, the present algorithm of this paper will be able to achieve at least “local optimality” with the present policy \(\pi ^{(t)}\), facilitating a gradual evolution toward the globally optimal policy with gradually better policy (i.e., \(\pi ^{(t)} \rightarrow \pi ^*, t\rightarrow \infty \)). This framework can embrace the existing geophysical approaches. For instance, the RL’s “state-transition probability” \(p:\mathcal {S}\times \mathcal {S}\times \mathcal {A}\rightarrow \mathbb {R}[0,1]\) is given by

Such state-transition probabilities are widely used in various forms in seismology since geophysicists derived the statistical rules such as ETAS^41,48 or Gutenberg-Richter law⁴² based on persistent observations of the EQ transitions over a long time. In the future extension, the existing statistical laws may help the proposed framework in the form of state-transition probability. The adopted GPRL is in spirit similar to the symbolic regression^49,50, which may provide more general (also complicated) forms of the prediction rules. For general forms, a future extension of Action Update Core may harness a deep neural network that takes input of all the aforementioned new features (e.g., \(\overline{II}, \mathcal {U}, \mathbb {K}, \mathbb {F}\)) and generates output of scalar action value. Since the policy determines actions for the given state, achieving consistently improving policy is vital for the reliable evolution of prediction models. The proposed learning framework is a “continuing” process, not an “episodic” one. Also, the state-transition \(S^{(t)}\rightarrow S^{(t+1)}\) (i.e., the transition from present EQ to future EQ at a location) is assumed to be stochastic and remains unknown. Therefore, future extensions may leverage general policy approximations and policy update methods⁵¹. The present state-action pair is a simple one-to-one mapping, and the present Q-value function is the simplest tabular form with clear interpretability. To accommodate complex relationships between states and actions, a future extension may find a general policy that is parameterized by \(\varvec{\uptheta }_{\pi }\), denoted as \(\pi (A^{(t)}|S^{(t)}; \varvec{\uptheta }_{\pi })\). A possibility of concurrent approximation and improvement of both Q-value function \(q(S,A;\varvec{\uptheta }_q)\) and policy \(\pi (A|S; \varvec{\uptheta }_{\pi })\), i.e., update of policy (actor) and value (critic) called actor-critic method⁴⁵.

Potential intellectual benefit from this paper’s outcomes.

The proposed AI seismogenesis agent will continue to evolve with clear interpretability, and machine learning-friendly data to be generated by this framework will accumulate. Toward the short-term deterministic large EQ predictions, this approach will add a meaningful dimension to our endeavors, empowered by data and AI. This AI framework will continue to enrich the new feature database which will accelerate the data- and AI-driven research and discovery about short-term large EQs. As depicted in Fig. 5, the proposed database will help diverse ML methods to explore and discover meaningful models about short-term EQs, importantly from data. Since the database will always preserve the physical meanings of each features, the resultant AI-driven models will offer (mathematically and physically) clear interpretations to researchers. The best-so-far AI-driven large EQ model will tell us which set of physics terms play a decisive role in reproducing the individual large EQ. Relative importance of the selected physics terms will be provided in terms of weights (e.g., in deep learning models) or mathematical expressions (e.g., in rule-learning models). These will substantially complement probabilistic or statistical models available in EQ forecasting/prediction methods of the existing research communities.

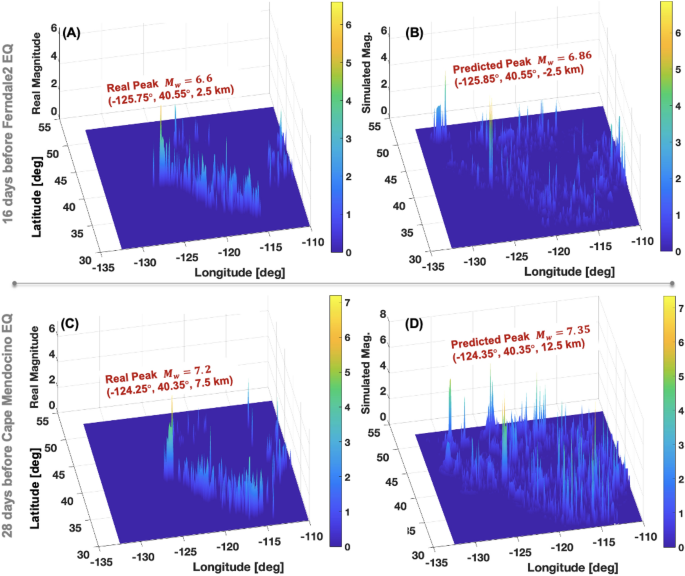
Another future research direction should include the generality of the proposed AI framework. Can the learned prediction rules apply to large EQ events in the untrained spatio-temporal ranges? If so, how reliable could the prediction be? To answer the general applicability of the AI framework is of fundamental importance since it will hint at a rise of practical large EQ prediction capability. This AI framework aims to establish a foundation for such a bold capability. Currently, the present research is dedicated to training the AI framework with the past four decades, generating new ML-friendly database, and accumulating new prediction rules. Still, we can glimpse the general applicability of the AI framework. Figure 6 shows examples of reasonably promising predictions of different temporal ranges (i.e., never used for training) with the best-so-far prediction rules. Some noisy false peaks are noticeable (Fig. 6B and D), but the overall prediction appears to be meaningful. It should be noted, however, that the majority of such blind predictions to other time ranges have failed to accurately predict the location and magnitude of large EQs (\(M_w\ge 5.5\)). This could be attributed to the early phase of the AI framework. As of August 2024, only 6.67% of total available EQ catalog between the year 1980 and 2023 are transformed into new ML-friendly features due mainly to the expensive computation cost even with the high-performance computing. If the AI framework continues expanding its coverage to all the available EQ catalog and learn more prediction rules, thereby enriching state and action sets, it may lead to practically meaningful generality in the not-too-distant future.

Examples of generality of the AI framework applied to different temporal regions: (A) Real observed EQ [Ferndale2 EQ, \(M_w=6.6\), February 19, 1995] and (B) the predicted EQ peaks by using the best-so-far prediction rules 16 days before the EQ. (C) Real observed EQ [Cape Mendocino EQ, \(M_w=7.2\), April 25, 1992] and (B) the predicted EQ peaks by using the best-so-far prediction rules 28 days before the EQ.

This paper holds transformative impacts in several aspects. This paper’s AI framework will (1) help transform decades-long EQ catalogs into ML-friendly new features in diverse forms while preserving basic physics and mathematical meanings, (2) enable transparent ML methods to distinguish and remember individual large EQs via the new features, (3) advance our capability of reproducing large EQs with sufficiently detailed magnitudes, loci, and short time ranges, (4) offer a database to which geophysics experts can facilely apply advanced ML methods and validate the practical meaning of what AI finds, and (5) serve as a virtual scientist to keep expanding the database and improving the AI framework. This paper will add a new dimension to existing EQ forecasting/prediction research.